Jacobian

Most text books provide a mathematical definition for the Jacobian. But I wonder if anyone understands what it really means?

Most of the robots have either revolute or prismatic joints or a combinations of both. Mathematically Jacobian is represented as \begin{equation} v_e = J \dot{q} \end{equation}

where \(v_e, ~\dot{q}\) and \(J\) are respectively the velocity of the end-effector ( a vector of dimension 6 x 1), velocity of the joints (of dimension n x 1) and Jacobian (of dimension 6 x n). Imagine a human arm and when the elbow joint is moved (keeping all other joints fixed), the fingers of our hand starts moving (or in more general the end-effector for a robot). If this process is repeated for other joints, it can be seen that each joint contributes a certain amount to the velocity of the end-effector. Jacobian quantifies each of these contributions in the form of a matrix and is dependant on the current joint position (q). It is easy to derive the Jacobian for a simple case to understand this idea.

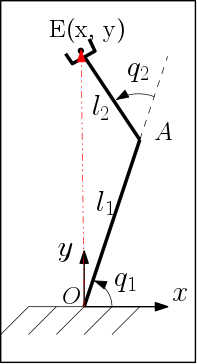
The end-effector co-ordinates can be found out as \begin{align} x &= l_1 \cos(q_1) + l_2 \cos(q_1 + q_2) \nonumber \newline % y &= l_1 \sin(q_1) + l_2 \sin(q_1 + q_2) \nonumber \newline % \theta &= q_1 + q_2 \end{align}

On taking the derivatives, \begin{align} \dot{x} &= - l_1 \sin(q_1) \dot{q_1} - l_2 \sin(q_1 + q_2) (\dot{q_1} + \dot{q_2}) \nonumber \newline % \dot{y} &= ~l_1 \cos(q_1) \dot{q_1} + l_2 \cos(q_1 + q_2) (\dot{q_1} + \dot{q_2}) \nonumber \newline % \dot{\theta} &= \dot{q_1} + \dot{q_2} \end{align} Rearranging the above, we can write the same equation as \begin{align} \begin{bmatrix} \dot{x} \nonumber \newline \dot{y} \nonumber \newline \dot{\theta} \end{bmatrix} = \begin{bmatrix} - l_1 \sin(q_1) - l_2 \sin(q_1 + q_2) & -l_2 \sin(q_1 + q_2)\nonumber \newline l_1 \cos(q_1) + l_2 \cos(q_1 + q_2) & l_2 \cos(q_1 + q_2)\nonumber \newline \nonumber \newline 1 & 1 \end{bmatrix} \begin{bmatrix} \dot{q_1} \nonumber \newline \dot{q_2} \end{bmatrix} \newline \nonumber \end{align} Note: This is a planar manipulator and hence the dimension of end-effector velocity is 3 x 1.

From the above it can be seen that the motion of joint 1 (\(q_1\)) would induce an x direction velocity of \(- l_1 \sin(q_1) - l_2 \sin(q_1 + q_2)\) to the end-effector and likewise in other directions. This Jacobian matrix so obtained is called the analytic jacobian. For most real world cases, analytical jacobian is hard to compute and the most common approach is to compute what is called the geometric jacobian. This main underlying concept of computing the geometrical jacobian is the equation \(v = r \times \omega\). In the above example, the instantaneous motion of joint 1 causes the end-effector to have a velocity of \(\hat{OE} \times \dot{q}_1\). Similarly \(\dot{q}_2\) contributes \(l_2 \times \dot{q}_2\) to the end-effector velocity.